前回は、「永久磁石のギャップ距離と空間磁束密度」について調べてみました。そこで今回は永久磁石と鉄板や永久磁石同士の吸引力が磁石の磁気特性、磁石の形状、磁石からの距離等とどのような関係があるのかをお話してみましょう。
<クーロンの法則と吸引力>
前回は、点磁極(磁荷)からのある距離の空間磁束密度は、原則として磁荷における「クーロンの法則」に関係していて、空間磁束密度は、(1)磁極の強さに比例し、(2)距離の二乗に反比例する、というお話をしました。そして、永久磁石の吸引力もまさにクーロンの法則に大きく関係してきます。
点磁極(磁荷)におけるクーロンの法則は、次のような式で表されることが知られています。磁極の強さをm1とm2[Wb]、2磁極間の距離をr[m]の透磁率をμ0とすれば、働く力の大きさF[N]は、F = m1m2/4πμ0r2 となります。m1の点磁極からは全方位、放射状に磁力線が出ていますから、m1から距離rでの位置は半径rの球体の表面ということになります。したがって、m2の位置は距離rの球体表面の一点になります。また、4πr2は次のような球体の表面積ということになります。
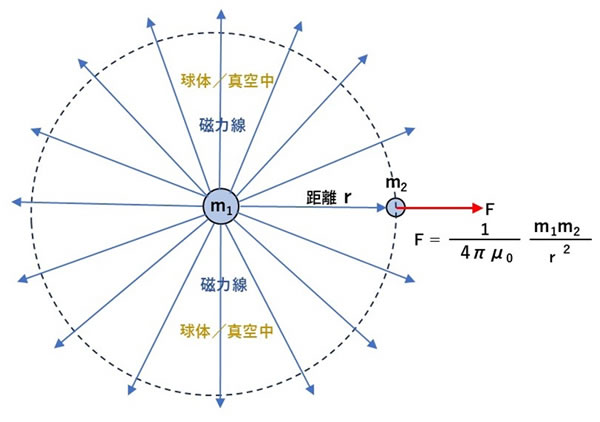
点磁極(磁荷)におけるクーロンの法則
<異方性永久磁石の吸引力>
ネオジム磁石を代表とする実用永久磁石の多くは一軸異方性磁石であり、磁化容易軸の一方向に磁化されています。したがって、前項で表したようなクーロンの法則をそのまま適用できません。しかし、磁石の吸引力にはクーロンの法則を反映した次のような関係があります。
(1)永久磁石の吸引力は磁束密度の二乗に比例する。
(2)永久磁石の吸引力は極面積に比例する。
この2種の原則より、標準磁石の鉄板への吸着力を測定しておいて、磁束密度(空間磁束密度)、極面積を比較して知りたい磁石の吸着力・吸引力を算出できます。なお、ギャップ距離は空間磁束密度に反映されます。
また、電磁石で利用される次のような近似式でもおおよその吸着力・吸引力の目安が算出できます。
F=KxBg2xS/2μ0 [N]
K:実測値とのずれ補正係数、Bg:ギャップ空間磁束密度(T)、S:磁極面積(m2)、μ0:真空(≒空気)の透磁率[4πx10-7(H/m)]
<各種条件下での吸引力>
次のグラフはA:磁石からXmm離れた距離の鉄板への吸引力、B:磁石に鉄板(バックヨーク)を付けた場合のXmm離れた距離の鉄板への吸引力、C:NS向かい合わせた磁石同士のXmm離れた距離の吸引力になります。ただし、鉄板は十分磁気飽和した鉄板であり、Cの2つの磁石は磁気特性、形状共に同等であることが条件です。
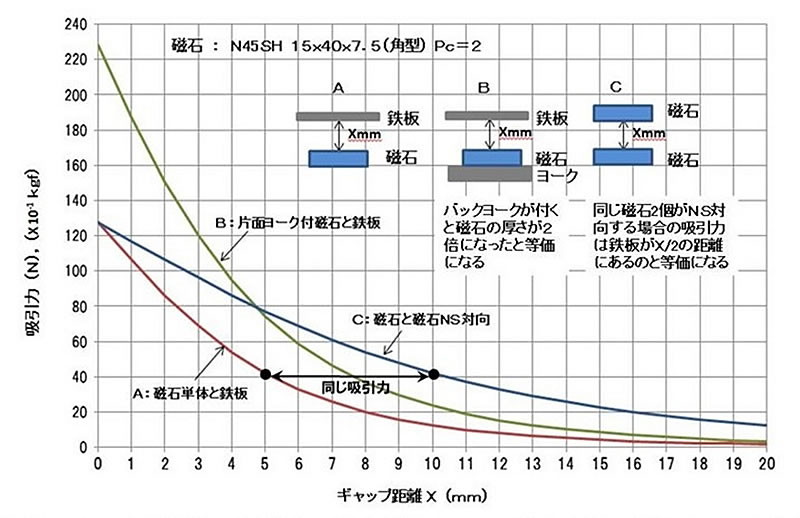
各種条件下でのギャップ距離と吸引力
なお、グラフ作成に使用した空間磁束密度の計算式は、「ネオジム磁石のすべて(14)」の角型磁石の近似式を参考にしました。
◆ギャップ距離ゼロの場合
ここで、皆さんは意外に思われるはずですが、距離ゼロではAの単体磁石と鉄板の吸引力とCの磁石同士の吸着力は同じになります。この理由は、磁束密度の比較の場合と同様、距離ゼロでは鉄板が相手の磁石により同じ強さで磁化して、磁石同士と同じことになるのです。
◆バックヨークを付けた場合
鉄板の吸引力はAの単体磁石の場合より、磁石にバックヨークを付けたBの方が距離ゼロであってもギャップ距離が大きくなっても強いことがわかります。これはバックヨークを付けることにより、磁石の磁化方向の厚みがほぼ2倍になったことと等価になり、パーミアンス係数が上がったためです。
◆NS向かい合わせた磁石同士の場合
NS向い合せた磁石同士のCをみると、距離ゼロでは単体磁石と鉄板の組み合わせAと同じ吸着力であったのが、ギャップが拡がるとはっきりその差がでてきます。空間磁束密度のページでご説明しましたように、向かい合った磁石同士では磁束のモレがないとすれば、その中間点の空間磁束密度は片方の磁石からみるとその位置に鉄板があるのと同じ値になります。したがって、NS向かい合った磁石同士の吸引力は、磁石間距離の2分の1の距離の磁石と鉄板の吸引力と同等になります。例えば、図に示しましたように、磁石と鉄板の距離が5mmと磁石と磁石同士の距離が10mmとはほぼ同じ吸引力になります。
このように、磁石間の吸引力は必ずしも磁石・鉄板間の吸引力の2倍になるわけではありません。距離によって、2倍以下の場合もあり、2倍以上になる場合もあります。
なお、NNまたはSS対抗の場合は、NS対向とは逆に反発力になり、磁束のモレがないとすれば磁石同士の反発力は吸着力と同様な関係がなりたちますが、実際は吸引力よりかなり弱くなります。

